

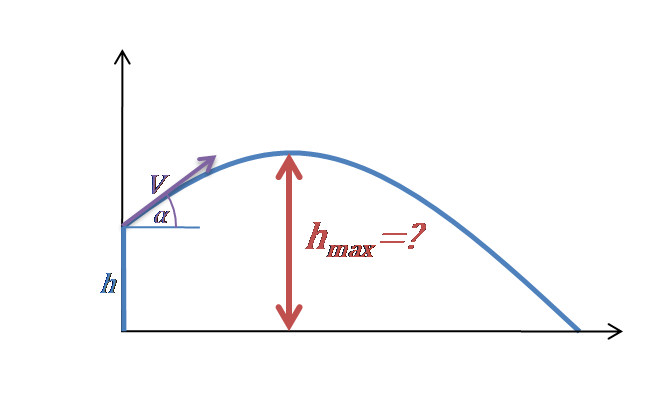
While the models used in these examples are simple, the concepts and interpretations are the same. You use displacement when you want to find out the distance from your original starting point to the final point of which you have travelled. In this section we introduced the concept of projectile motion, and showed that it can be modeled with a quadratic polynomial. TJ 11 years ago You use distance when you want to find the length that was travelled by an object. The video that follows presents another example of solving a quadratic equation that represents parabolic motion. Interpret: It doesn’t make sense for us to choose t=0 because we are interested in the amount of time that has passed when the projectile is 4 feet from hitting the ground on it’s way back down. Translate: So, we will substitute 0 for h in the formula and solve for t. Lesson 1: Position and Velocity in 2D Space - Part 1. We want to know how long, t, the rocket is in the air. Covers an acceleration, velocity, and position in 2D space, circular motion and projectile motion. Optimal angle for a projectile part 3: Horizontal distance as a function of angle (and speed) Optimal angle for a projectile part 4: Finding the optimal angle and distance with a bit of calculus. Optimal angle for a projectile part 2: Hangtime. Here is what they came up with.Read and understand: The rocket will be on the ground when the height is 0. Optimal angle for a projectile part 1: Components of initial velocity. The variables include acceleration (a), time (t). Kids were coming up with some hilarious scenarios, and enjoying a math problem. v 2 v 0 2 + 2 a (x x 0) v 2 v 0 2 + 2 a (x x 0) Table 5.1 Summary of Kinematic Equations (constant a) Where x is position, x 0 is initial position, v is velocity, v avg is average velocity, t is time and a is acceleration. Kinematic equations relate the variables of motion to one another. To find the range, we find the coordinates of the vertex of y x 2 6 x 5 (either using. This predictable motion has been studied for centuries, and in simple cases, an object’s height from the ground at a given time, t t, can be modeled with a polynomial function of the form h(t) at2 +bt+c h ( t) a t 2 + b t + c, where h(t) h ( t) represents the height. As I walked around I heard one students say things like, “No, the rocket doesn’t start at the ground because you can’t start at negative time.” I loved this part because of the conversations but especially because of the laughter. Projectile Motion Calculator>Projectile Motion Calculator. A projectile will follow a curved path that behaves in a predictable way. I told them they could write it, or draw a picture, or both.Īfter they created their stories I had them share with the rest of the class. I told my students to create a story with their team from this graph, using as much information as they could from the picture (below). I did not follow her fireworks task exactly. As soon as I saw this graph, I knew I had to use it! I loved how Sara described clicking on one aspect at a time. I had planned on making up my own scenario, until I saw this terrific post by Sara Vanderwerf that involved a creative fireworks graph. So today, before I taught them about the equation, I gave them a picture of a quadratic graph. They get all caught up in the particulars of the formula and stop thinking about what is actually happening. I like for them to discover things! They often make “much ado about nothing” when it comes to the projectile motion equation in Algebra 2, even though it should make sense to them. Well, I say that, but I hate to actually TELL them anything. Today I taught my students about projectile motion.


 0 kommentar(er)
0 kommentar(er)
